I was helping someone recently with advice about a good basic strategy for doing sensitivity analysis with an economic model. Here is my advice.

Sensitivity analysis is the official term for “what if” analysis. It’s one of the things that makes economic models so useful. We know that any given model is not totally accurate, and that the variables that drive it will vary somewhat unpredictably over time, but using sensitivity analysis we can still get useful information and insight from the model. It helps you to get a feel for the stability of results, identify the factors that most affect results, and estimate the probability of a strategy performing up to a required level.

I quite often see studies where sensitivity analysis has been done quite poorly … What if this? What if that? … with insufficiently systematic thought about which variables to look at or how to vary them.

This Pannell Discussion provides a suggested procedure for conducting and reporting a useful sensitivity analysis. It is not perfect or universally applicable, and it may need to be adapted depending on the nature of your analysis. It’s meant to be a fairly simple standard approach that will work quite well in many cases. More detail is provided in Pannell (1997).

1. Decide which are the key results you are interested in from your model. Go back to the core question driving your analysis when thinking about this. Depending on the purpose of the analysis, it might be the economic returns (e.g. net profit or Net Present Value ), the difference between economic returns between two strategies or two scenarios, or the optimal level of a particular practice within the overall strategy. For later parts of the sensitivity analysis, you may need to think about how to capture the key results in a few numbers, possibly even in a single number.

2. Identify the parameters of the model that may influence its results.

3. Specify low, best-bet and high values for each of these parameters. Low and high should be for a one-year-in-five or one-year-in-10 scenario. Make the range of values a bit wider than you think. Often we don’t sufficiently expect the unexpected.

4. Solve the model for low and high values of each parameter, varying one parameter at a time and setting all others at their best-bet values. Choose say the six parameters that make the biggest difference to the key model result(s). Key model results might be Net Present Value (NPV) and Benefit:Cost Ratio (BCR), or it might the impact on NPV of a change in management.

5. For those six parameters, specify probabilities for the low, best-bet and high values. These probabilities must add to 1. Depending on how you specify the low and high parameter values, the probabilities could perhaps be [0.1, 0.8, 0.1]; or [0.2, 0.6, 0.2]; or [0.25, 0.5 and 0.25]. The parameter values for the first set of probabilities would be more widely spread than for the last set.

6. Generate model results for every combination of the 6 parameters – i.e. 3⁶ = 729 sets of model results (or if that’s too many to handle, do it for five parameters: 3⁵ = 243). Store them in a big table where the columns represent: the values of each parameter, the key model results for that scenario (e.g. NPV and BCR) and the joint probability of that result. Usually it is reasonable to assume that the distributions of the parameters are independent, so that the joint probabilities are just the products of each of the relevant probabilities.

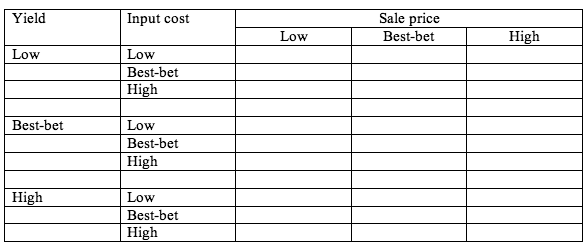
7. Create a series of small tables that show a selection of results for say three parameters (ignoring probabilities for now). These tables just show how key results vary in a simple way. The variables not depicted in the table would be set at their best-bet values. The user could select two or three of these tables for inclusion in the report for the analysis. The format for each one would be as follows (in this example, the parameters of interest are called Sale price, Yield and Input cost):

8. For each value of each of the six parameters, take the weighted average of the results for all other results, as follows. Suppose the one of the six parameters is “sale price”. There are 243 results that include a low sale price. Take the weighted average of those 243 results using their conditional probabilities (i.e. conditional on a low sale price – to get the conditional probabilities, divide the individual probabilities of the 243 results by the probability of a low sale price). Repeat this process for Best-bet and High values of sale price. Plot the three results on a graph, with the X axis representing low, best-bet and high values of the parameter. Show these as “Low”, “Best-bet” and “High” rather than numerical values. Repeat that process for all 6 parameters. Plot them all on the same graph to create a so-called spider diagram. This indicates which parameters have the biggest influence on results. Do this in separate graphs for each of the key outputs (e.g. NPV and BCR). This spider diagram is better than the one you would have got if you had graphed the results of step 3 because it allows for the possibility that there will be strong interactions between parameters. In that case, you cannot judge things by varying one parameter at a time, but this approach of looking at all possible combinations will give you a good understanding of things.

9. Create a table that shows the average difference between high and low results for each parameter (from step 7) as a sort of sensitivity index. Rank the parameters by their sensitivity index values. Repeat for each key model output (e.g. BCR and NPV).

10. Finally, generate cumulative probability distribution functions for each key output. This will allow the user to see the probability of the result exceeding a specified threshold level (e.g. the probability that BCR will be at least 2). To do this graph for say BCR, from the big table from step 5, take all the BCR and probability values, sort them by BCR from lowest to highest, and then calculate cumulative probability. Then convert them to numbers rather than equations and store them somewhere. Plot BCR on the X axis and cumulative probability on the Y axis.

Reporting the analysis

(a) In the methods section, present a table showing the low, best-bet and high parameter values, and a table showing their probabilities (or if they are the same for each parameter, just describe the probabilities in the text of the methods section).

(b) In the results section, start by presenting results for the base-case model, including only best-bet values of parameters. Describe and discuss this in some detail.

(c) Maybe present results for one or two other scenarios in moderate detail. This can be useful if there are what-if scenarios that you want to look at that can’t easily be represented by simple parameter changes.

(d) Present the two or three tables from step 7. Describe and discuss any interactions that are apparent.

(e) Present the spider diagram(s) from step 8. Discuss which variables have the biggest influence and the nature of that influence (positive, negative, linear, non-linear)

(f) Maybe present the table from step 9 (although you may think that the spider diagram is sufficient).

(g) Present the cumulative probability function diagram(s) from step 10. Describe and discuss the probabilities of outputs achieving relevant threshold levels, such as breaking even.

(h) If there is space, include the big table from step 6 in an appendix.

This provides a good standard set of sensitivity analysis results that should give you all you practically need in many cases.

David Pannell, The University of Western Australia

Further Reading

Pannell, D.J. (1997). Sensitivity analysis of normative economic models: Theoretical framework and practical strategies. Agricultural Economics 16: 139-152. Full paper (100 K)